Codeforces Round 1012 (Div. 2) C. Dining Hall.
The problem statement
An infinite grid in the positive quadrant, that is, extending only in positive \(x\) and \(y\) axes, is said to contain some tables. Each table is a sub-grid of dimension \(2 \times 2\) starting at coordinates \((3x+1, 3y+1)\). Each of the four cells of a sub-grid is treated as a seat for a guest.
The configuration of the tables leaves a row and a column empty between any two tables. Those empty rows and columns are treated as corridors for guest movement. Each guest starts from cell \((0,0)\) and walks the shortest distance to their chosen cell by moving only right or up through the corridors.
Guests arrive one by one, and each guest chooses a table cell based on their type. There are two types of guests, type \(0\) and type \(1\).
- Type \(0\) guests always choose the closest available unoccupied table.
- Type \(1\) guests always choose the closest available table.
Given a sequence of guests, the problem asks to output the coordinates of the cell they take.
Initial observations
At first, let’s focus on a single table and try to figure out a formula for the shortest distance to any cell.
- For the three cells, except the top-right one, distance is obvious, and it is \(x+y\), because a guest can always reach those cells traversing \(x\) columns and \(y\) rows through the corridors.
- For the top-right cell, the distance is \(x+y+2\), because a guest has to move one additional column or row ahead and then get back.
It is also obvious that type \(0\) guests always choose the bottom-left cells of tables, because they have the shortest distance among the four cells in a table.
Ordering cells by distance
Now that we know the distance formula for cells, which cell do we allocate each incoming guest? For simplicity, let’s focus only on the simpler, that is, type \(1\) guests, case first. Keeping track of already occupied cells and performing an exhaustive search for the next closest cell for each guest would be inefficient.
Let’s try to figure out the pattern of distances of the cells. There is an obvious pattern in a single table: from the bottom-left cell \((x,y)\), the next distant two cells are the next one along \(y\) axis, \((x,y+1)\), and the next one along the \(x\) axis, \((x+1,y)\), with a distance difference of \(1\). The next closest is the diagonal opposite one, \((x+1,y+1)\), with a distance difference of \(4\).
However, fixing attention on the first table, we can see that after \((x,y+1)\) and \((x+1,y)\), the \((x+1,y+1)\) cell in the same table is not the next closest cell overall. The next closest cells are actually in the next two tables along the \(x\) and \(y\) axes, namely, \((x+2,y)\) and \((x,y+2)\), both with a distance difference of \(3\) from \((x,y)\). Also note that those two cells are the bottom-left cells of their respective tables.
Deeper look into cell distance ordering
Let’s try to figure out a pattern visually by drawing the grid with distances of each cell marked.
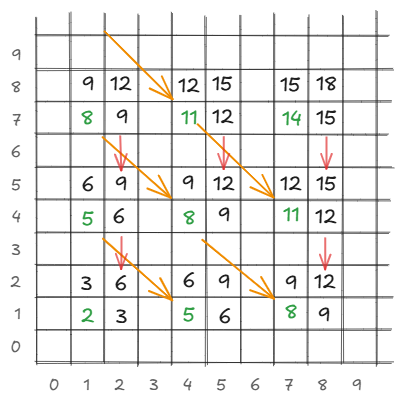
The following table that groups the cells by their distances is the summary of the visual observation:
| # | Cells | Distance |
|---|---|---|
| 1 | \((1,1)\) | \(2\) |
| 2 | \((1,2)\), \((2,1)\) | \(3\) |
| 3 | \((1,4)\), \((4,1)\) | \(5\) |
| 4 | \((1,5)\), \((2,2)\), \((2,4)\), \((4,2)\), \((5,1)\) | \(6\) |
| 5 | \((1,7)\), \((4,4)\), \((7,1)\) | \(8\) |
| 6 | \((1,8)\), \((2,5)\), \((2,7)\), \((4,5)\), \((5,2)\), \((5,4)\), \((7,2)\), \((8,1)\) | \(9\) |
| 7 | \((1,10)\), \((4,7)\), \((7,4)\), \((10,1)\) | \(11\) |
| 8 | \((1,11)\), \((2,8)\), \((2,10)\), \((4,8)\), \((5,5)\), \((5,7)\), \((7,5)\), \((8,2)\), \((8,4)\), \((10, 2)\), \((11, 1)\) | \(12\) |
The odd rows in the preceding table are of particular interest. They contain only the bottom-left cells of the tables and show the following interesting properties:
- Starting from cell \((1,1)\), elements grow by \(1\) and distance increases by \(3\) in each step.
- The cells’ coordinates also have an obvious pattern: \(x \mod 3 = 1\) and \(y \mod 3 = 1\), and \(x+y\) equals the distance.
- Each odd row dictates both the next odd row and also the next even row, and the rule continues successively, like a chain reaction.
The even rows have the following properties:
- The even rows have a distance increasing by \(1\) from the preceding odd row, and like the odd rows, their distance also increases by \(3\) in each step.
- Each odd row cell, that is, a bottom-left cell, \((x,y)\), produces two or three cells in the next even row with the same distance:
- One along the \(y\) axis, \((x,y+1)\) and one along the \(x\) axis, \((x+1,y)\).
- If \(y-2>0\), that is, the top-right cell of the table immediately below \((x+1,y-2)\).
- Note here, the top-right cell in the table immediately below, if it exists, comes next to \((x,y+1)\), according to the order dictated by the problem statement.
- The cell coordinates follow this pattern: \(x\) and \(y\) are congruent to either \(1\) or \(2\) modulo \(3\).
Solution
- Precompute the table described in the preceding section using the rules described there up to a reasonable limit, covering the maximum number of guests.
- Keep track of the next type \(0\) cell and type \(1\) cell separately in two variables. Initialize both to \((1,1)\).
- After that, for each incoming guest, find out a seat from the precomputed table using the following rules:
- For type \(1\) guests, simply move to the next element in the precomputed list.
- For type \(0\) guests, move to the next bottom-left cell, by checking \(x \mod 3 = 1\) and \(y \mod 3 = 1\).
- When updating the next type \(1\) cell take care of the following:
- If the next type \(1\) cell is a bottom-left one and the next type \(0\) cell is already past that, then the cell has already been occupied by a type \(0\) guest. Skip the cell and move to the next in these cases.
- Check if the next type \(1\) cell went past the next type \(0\) cell. If it did, move the next type \(0\) cell to the next table after \(1\).

